Colloidal Self-Assembly
We investigate how particles form complex structures.
- Colloidal clusters
- Phase behavior of hard sphere mixtures
- Self-assembly of nanocrystals
- Complexity with pair potentials
Colloidal clusters
Clusters in systems as diverse as metal atoms, virus proteins, noble gases, and nucleons have properties that depend sensitively on the number of constituent particles. Certain numbers are termed ‘magic’ because they grant the system with closed shells and exceptional stability. To this point, magic number clusters have been exclusively found with attractive interactions as present between atoms. We showed that magic number clusters exist in a confined soft matter system with negligible interactions. Colloidal particles in an emulsion droplet spontaneously organize into a series of clusters with precisely defined shell structures. Crucially, free energy calculations demonstrated that colloidal clusters with magic numbers possess higher thermodynamic stability than those off magic numbers.
-
Junwei Wang, Umair Sultan, Eric S. A. Görlitzer, Chrameh F. Mbah, Michael Engel, Nicolas Vogel
Structural Color of Colloidal Clusters as a Tool to Investigate Structure and Dynamics
Advanced Functional Materials 30, 1907730 (2020) -
Junwei Wang, Chrameh F. Mbah, Thomas Przybilla, Silvan Englisch, Erdmann Spiecker, Michael Engel, Nicholas Vogel
Free Energy Landscape of Colloidal Clusters in Spherical Confinement
ACS Nano 13, 9005-9015 (2019) -
Junwei Wang, Chrameh F. Mbah, Thomas Przybilla, Benjamin Apeleo Zubiri, Erdmann Spiecker, Michael Engel, Nicolas Vogel
Magic Number Colloidal Clusters as Minimum Free Energy Structures
Nature Communications 9, 5259 (2018)

Phase behavior of hard sphere mixtures
Colloids are rarely perfectly uniform but follow a distribution of sizes, shapes, and charges. This dispersity can be inherent (static) or develop and change over time (dynamic). Despite a long history of research, the conditions under which nonuniform particles crystallize and which crystal forms is still not well understood. We demonstrated that binary and even size-disperse hard sphere mixtures crystallize readily if compressed slowly enough, and they do so in surprisingly complex ways. This result was obtained by accelerating event-driven simulations with particle swap moves for static dispersity and particle resize moves for dynamic dispersity.
-
Praveen K. Bommineni, Marco Klement, Michael Engel
Spontaneous Crystallization in Systems of Binary Hard Sphere Colloids
Physical Review Letters 124, 218003 (2020) -
Praveen K. Bommineni, Nydia Roxana Varela-Rosales, Marco Klement, Michael Engel
Complex Crystals from Size-Disperse Spheres
Physical Review Letters 122, 128005 (2019)

Self-assembly of nanocrystals
Nanocrystals can be prepared via chemical synthesis with highly uniform size and shape. They move by Brownian motion and are building blocks for self-assembly processes to create functional materials. Applications rely on the unique optical, magnetic, electronic, and catalytic properties of individual nanoparticles as well as their assemblies. We have developed geometric models and computational methods to derive and validate fundamental principles governing nanocrystal self-assembly. We investigate important design parameters such as particle shape, anisotropic interactions, and the role of the assembly environment.
-
Haixin Lin, Sangmin Lee, Lin Sun, Matthew Spellings, Michael Engel, Sharon C. Glotzer, Chad A. Mirkin
Clathrate Colloidal Crystals
Science 355, 931-935 (2017) -
Jianxiao Gong, Richmond S. Newman, Michael Engel, Man Zhao, Fenggang Bian, Sharon C. Glotzer, Zhiyong Tang
Shape-Dependent Ordering of Gold Nanocrystals into Large-Scale Superlattices
Nature Communications 8, 14038 (2017) -
Xingchen Ye, Jun Chen, M. Eric Irrgang, Michael Engel, Angang Dong, Sharon C. Glotzer, Christopher B. Murray
Quasicrystalline Nanocrystal Superlattice with Partial Matching Rules
Nature Materials 16, 214-219 (2017) -
Michael A. Boles, Michael Engel, Dmitri V. Talapin
Self-Assembly of Colloidal Nanocrystals: From Intricate Structures to Functional Materials
Chemical Reviews 116, 11220-11289 (2016) -
Kaylie L. Young, Michelle L. Personick, Michael Engel, Pablo F. Damasceno, Stacey N. Barnaby, Reiner Bleher, Tao Li, Sharon C. Glotzer, Byeongdu Lee, Chad A. Mirkin
A Directional Entropic Force Approach to Anisotropic Nanoparticle Assembly
Angewandte Chemie 52, 13980-13984 (2013) -
Xingchen Ye, Jamie A. Millan, Michael Engel, Jun Chen, Benjamin T. Diroll, Sharon C. Glotzer, Christopher B. Murray
Shape Alloys of Nanorods and Nanospheres from Self-Assembly
Nano Letters 13, 4980-4988 (2013) -
Xingchen Ye, Jun Chen, Michael Engel, Jamie A. Millan, Wenbin Li, Liang Qi, Guozhong Xing, Joshua E. Collins, Cherie R. Kagan, Ju Li, Sharon C. Glotzer, Christopher B. Murray
Competition of Shape and Interaction Patchiness for Self-Assembling Nanoplates
Nature Chemistry 5, 466-473 (2013)

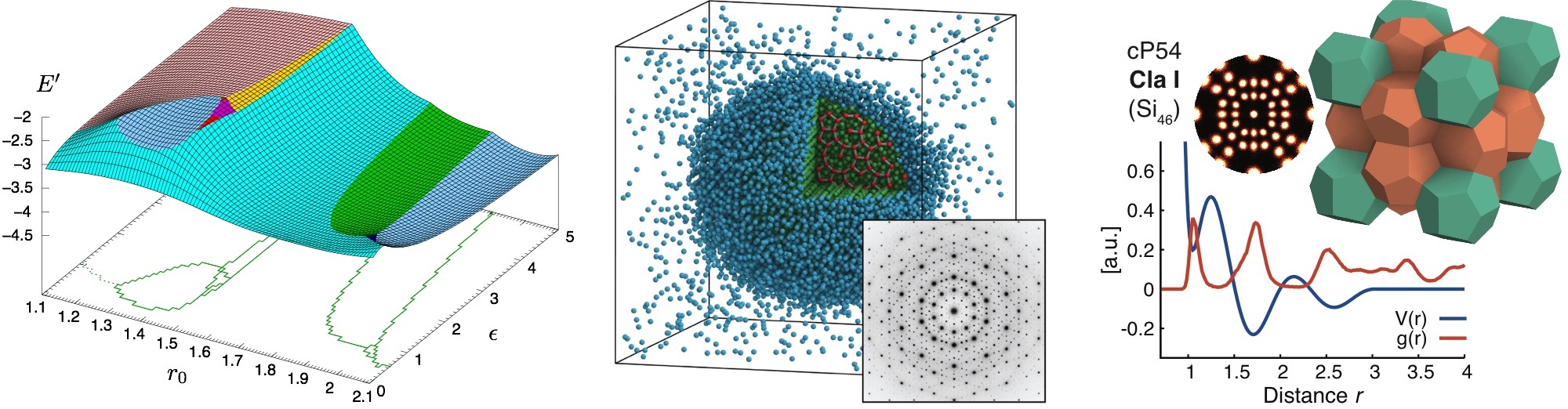
Complexity with pair potentials
The interaction of atoms and soft colloids is frequently modeled using effective classical pair potentials. This allows studying their thermodynamics, phase behavior, and transport phenomena. Pair potentials with just one length scale are common models for many gases and simple fluids and well established, but complex fluids and crystallization into non-close-packed crystals require angular terms or multiple length scales. Important findings so far are the first computational self-assembly of an icosahedral quasicrystal and clathrates from molecular dynamics simulations.
-
Julia Dshemuchadse, Pablo F. Damasceno, Carolyn L. Phillips, Michael Engel, Sharon C. Glotzer
Moving Beyond the Constraints of Chemistry via Crystal Structure Discovery with Isotropic Multiwell Pair Potentials
Proceedings of the National Academy of Sciences 118, e2024034118 (2021) -
Michael Engel, Pablo F. Damasceno, Carolyn L. Phillips, Sharon C. Glotzer
Computational Self-Assembly of a One-Component Icosahedral Quasicrystal
Nature Materials 14, 109-116 (2015) -
Michael Engel, Hans-Rainer Trebin
Structural Complexity in Monodisperse Systems of Isotropic Particles
Zeitschrift für Kristallographie 223, 721-725 (2008) -
Michael Engel, Hans-Rainer Trebin
Self-Assembly of Monatomic Complex Crystals and Quasicrystals with a Double-Well Interaction Potential
Physical Review Letters 98, 225505 (2007)