High-Performance Algorithms

We develop simulation algorithms with superior performance.

Newtonian event-chains

An important task in the simulation of hard spheres and other hard particles is structure prediction via equilibration. Event-driven molecular dynamics is efficient because its Newtonian dynamics equilibrates fluctuations with the speed of sound. Monte Carlo simulation is efficient if performed with correlated position updates in event chains. We combined the core concepts of molecular dynamics and event chains into a new algorithm involving Newtonian event chains (NEC). NEC scale well to large systems and can be extended to anisotropic hard particles without approximations. NEC is currently the fastest available hard particle simulation algorithm. Recently, the NEC algorithm was extended to polyhedral and parallelized.

Newtonian Event Chains
Schematic overview of simulation algorithms for hard spheres.

Large-scale parallel Monte Carlo simulations

Current trends in parallel processors call for the design of efficient massively parallel algorithms for scientific computing. Parallel algorithms for Monte Carlo simulations of thermodynamic ensembles of particles have received little attention because of the inherent serial nature of the statistical sampling. With Joshua Anderson we devised a massively parallel method that obeys detailed balance and implement it for a system of hard disks on the graphics processors (GPUs). We applied the method to elucidate the nature of the two-dimensional melting transition of hard disks and polygons.

Large-Scale Monte Carlo
(Left) Schematic of cell decomposition (Right) Equation of state of the hard disk system near coexistence of fluid and solid. (Right) Local density at different global densities.

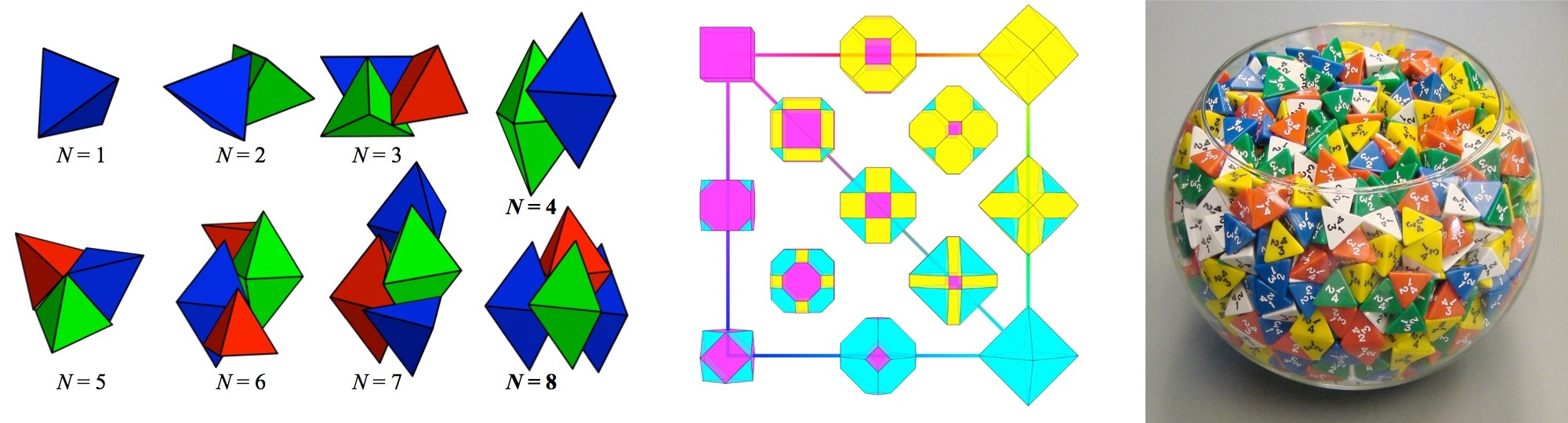
Maximization of packing density

A packing problem is an optimization problem that asks how to pack objects in space. Packing problems are easy to grasp and notoriously hard to solve. Recent work on nanoparticle and colloidal self-assembly, jammed granular matter, and biological cell aggregation and crowding further motivated the study of packings. Packing in containers has applications in operations research, such as optimal storage, packaging, and transportation. We discovered the densest packing of tetrahedra and studied a three-parameter family of symmetric polyhedra using a simulated annealing algorithm.

Densest Packing
(Left) Densest packings of tetrahedra in periodic boxes. (Middle) Two-parameter family of shapes. (Right) Bowl of tetrahedral dice.